

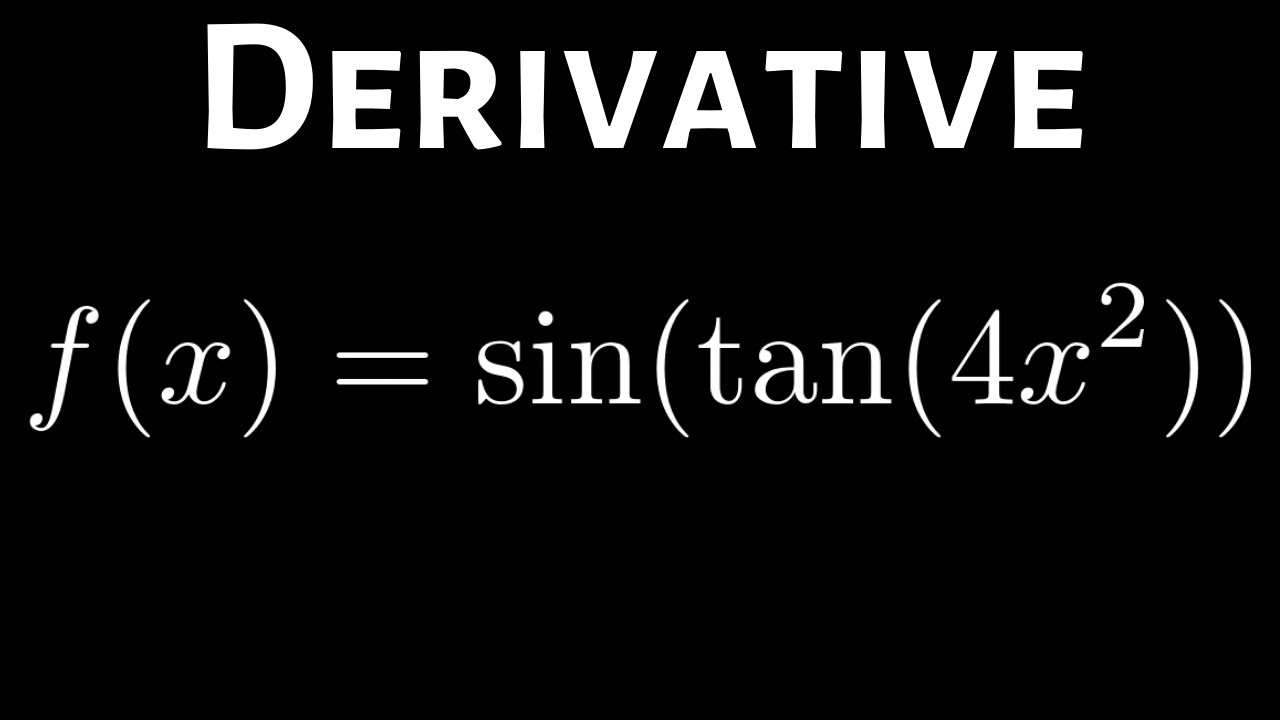

A technique that is sometimes suggested for differentiating composite functions is to work from the “outside to the inside” functions to establish a sequence for each of the derivatives that must be taken.Įxample 1: Find f′( x) if f( x) = (3x 2 + 5x − 2) 8.Įxample 2: Find f′( x) if f( x) = tan (sec x).Įxample 5: Find the slope of the tangent line to a curve y = ( x 2 − 3) 5 at the point (−1, −32).īecause the slope of the tangent line to a curve is the derivative, you find that Here, three functions- m, n, and p-make up the composition function r hence, you have to consider the derivatives m′, n′, and p′ in differentiating r( x). For example, sin(x) is a composite function because it can be constructed as f(g(x)) for f(x)sin(x) and g(x)x. In other words, it helps us differentiate composite functions. If a composite function r( x) is defined as The chain rule states that the derivative of f(g(x)) is f'(g(x))g'(x). Note that because two functions, g and h, make up the composite function f, you have to consider the derivatives g′ and h′ in differentiating f( x). For example, if a composite function f( x) is defined as The function f(x) is simple to differentiate because it is a simple. We just took the derivative with respect to x by following the most basic differentiation rules. What does that mean Lets start with an example: f(x) 4x2 + 7x 9 f (x) 8x + 7. This can be simplified of course, but we have done all the calculus, so that only algebra is left. The chain rule provides us a technique for finding the derivative of composite functions, with the number of functions that make up the composition determining how many differentiation steps are necessary. The chain rule allows us to differentiate a function that contains another function. Volumes of Solids with Known Cross Sections.Second Derivative Test for Local Extrema.First Derivative Test for Local Extrema.Differentiation of Exponential and Logarithmic Functions Given f(x) left(3x2 - 4x + 5right)8, f(x) Chain Rule Problem 2.Differentiation of Inverse Trigonometric Functions.Limits Involving Trigonometric Functions.


 0 kommentar(er)
0 kommentar(er)
